Exploring JavaScript - Time Complexity of Array Insertion Methods
1. Introduction
JavaScript arrays are not actual arrays. So what is the time complexity of the array insertion methods?
1.1. Question
In general programming languages, an array is a data structure that stores elements in contiguous memory spaces. Therefore, in languages like C, arrays are declared with a fixed size, determining the extent of contiguous memory space to use, and resizing an array is typically not possible.
For example, if an array of size 10 is declared in C, it cannot subsequently be resized to 11 or any other size. Even with dynamic arrays, one must allocate a new array and copy the existing array to it.
However, JavaScript arrays are not actual arrays. They are objects, and the indices of arrays are properties of these objects. It is possible to add properties other than indices and to increase or decrease the size of the array. Methods such as push, pop, shift, and unshift exist.
Of course, there are similar data structures in other languages. For instance, Python's list or C++'s Vector is implemented as dynamic arrays. However, they are intriguingly different from JavaScript's arrays, which have key-value pairs.
So, what is the time complexity of the insertion methods for JavaScript arrays? Do they have a time complexity similar to that of dynamic arrays like C++'s Vector? Or can they allow O(1) insertion on both ends by using different data structures?
Therefore, this article analyzes the time complexity of JavaScript array insertion methods based on specifications that all JavaScript engines must follow and benchmarking.
We will later see in detail how arrays are implemented in JavaScript, but it is evident that JavaScript arrays are implemented as arrays occupying contiguous memory space in most engines. However, alternative implementations do exist, and in certain cases, the internal structure may be converted to other data structures. Hence, this article analyzes the time complexity based on specifications.
2. Specification Exploration
2.1. push
The push method of an array adds an element to the end of the array. It is represented in the form Array.prototype.push(element1, element2, ...), adding all the received arguments to the end of the array and returning the new length of the array.
The specification of Array.prototype.push in ECMA-262 is as follows.

By ignoring error checking and focusing on the logic, it repeatedly adds the received arguments to the end of the array and increments the array length by 1 for each argument. Therefore, the time complexity can be considered O(number of arguments), and if the number of arguments is constant, it is O(1).
2.2. pop
Array.prototype.pop removes the element at the end of the array, specifically the element at index array.length - 1, and returns the removed element. The specification in ECMA-262 is as follows.

There is a condition to return undefined when the array is empty. Nonetheless, the basic logic here is to remove and return the last element of the array without performing any operations on other elements. Therefore, the time complexity is O(1).
2.3. unshift
Array.prototype.unshift adds the received elements to the front of the array and returns the new length of the array. The specification is as follows.
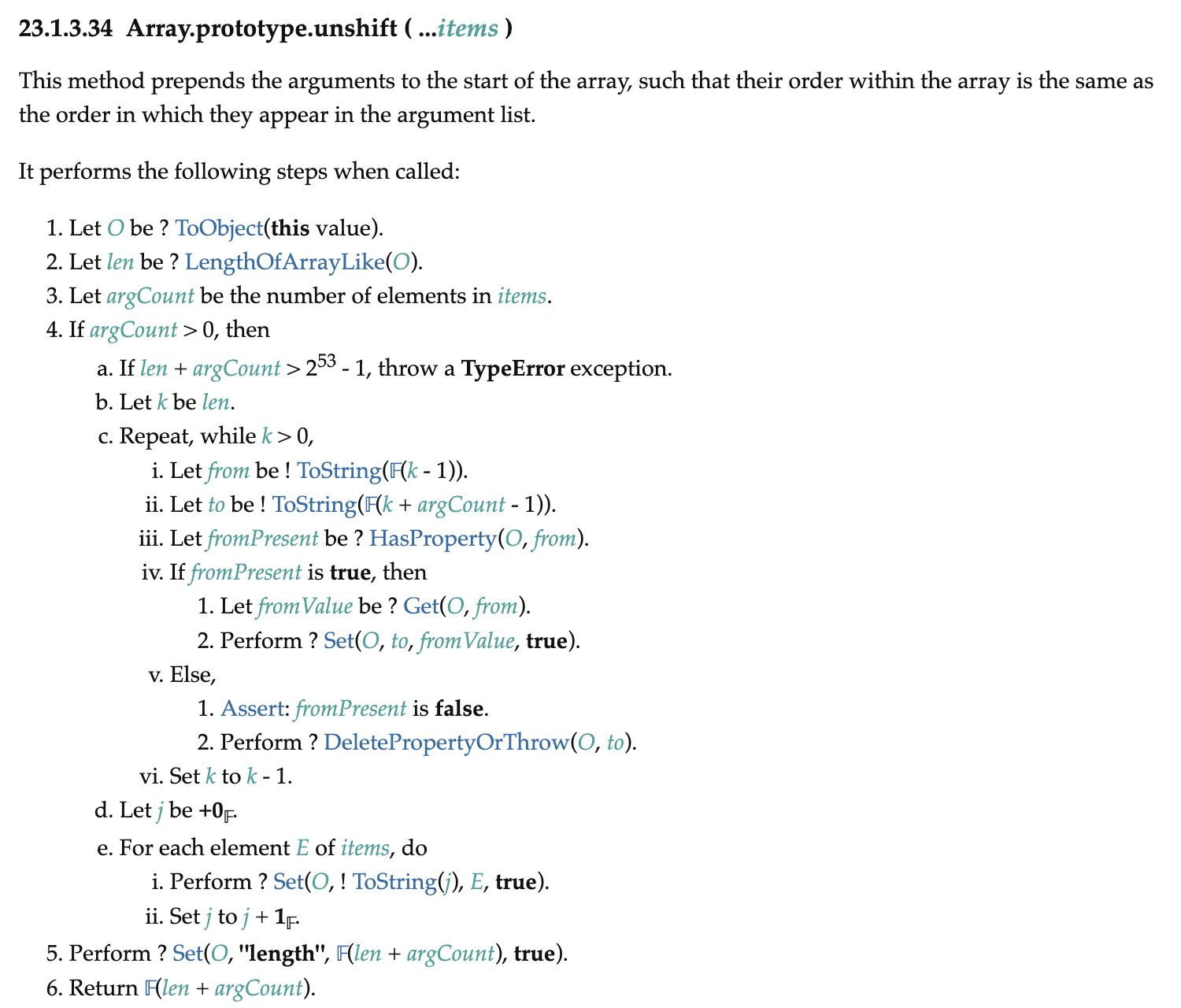
In section 4.c, it can be seen that the existing elements of the array are shifted back by the number of arguments, argCount. Then, the elements received as arguments are added to the front of the array (which is now empty since the existing elements have been moved).
The time complexity of this function is O(length of existing array + number of unshifted arguments), and since the number of unshift arguments is generally less than the length of the existing array, it can be said that the time complexity is O(n).
2.4. shift
Array.prototype.shift removes the element at the front of the array and returns the removed element. The specification is as follows.

Here, in point 6, it indicates that the existing elements are shifted forward by one position. Elements in the index range [1, len-1] are moved to the index range [0, len-2]. There are no other iterative operations applied beyond this.
Thus, the time complexity of this function can be considered O(length of the existing array), which means it is O(n). The first element of the existing array must be returned later, so it is stored temporarily in point 4 and returned in point 9.
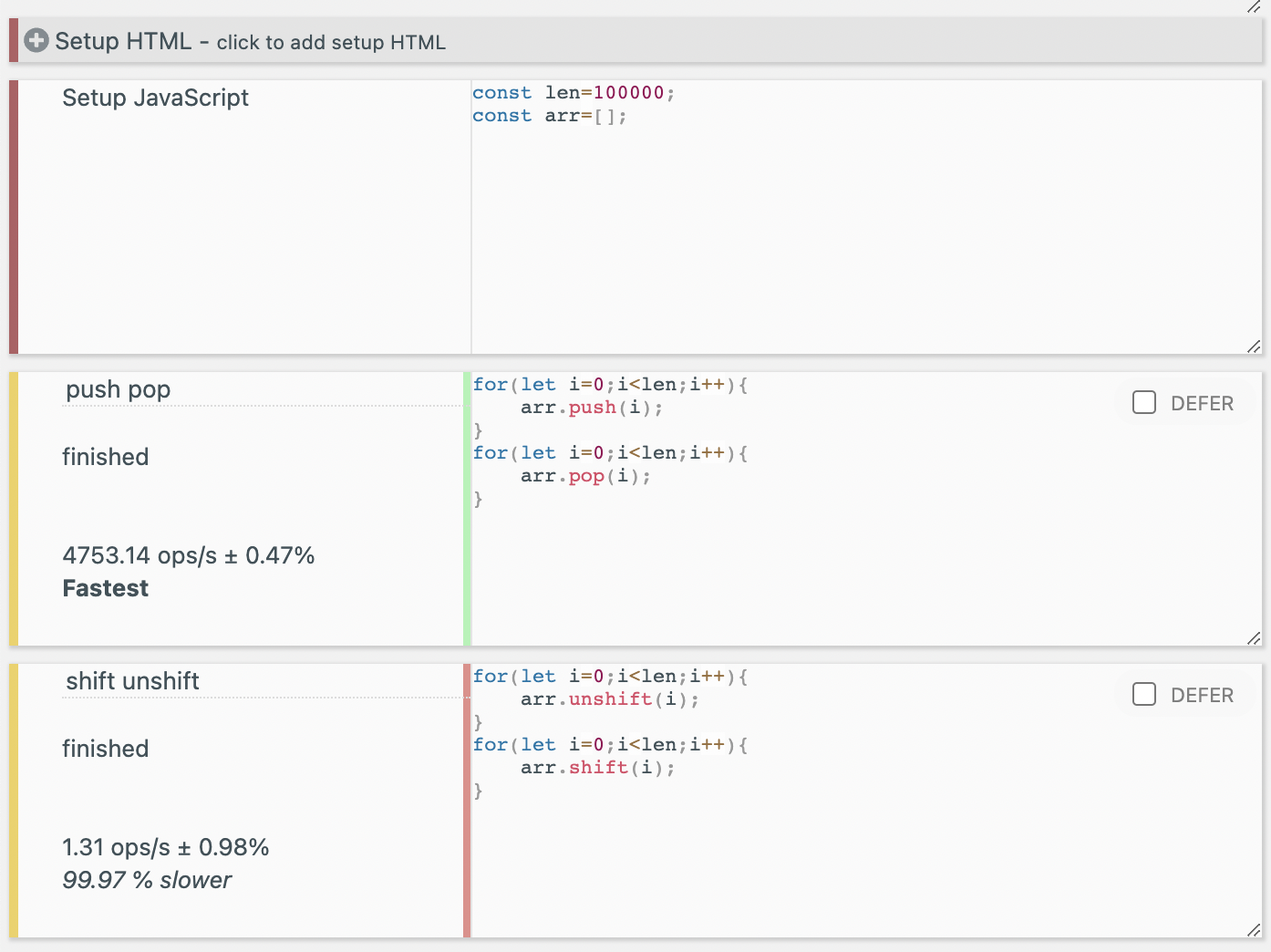
3. Benchmarking
A simple benchmark was also conducted using the JS Benchmark site. Initially, it was run about 1000 times. It was observed that push and pop were significantly faster.
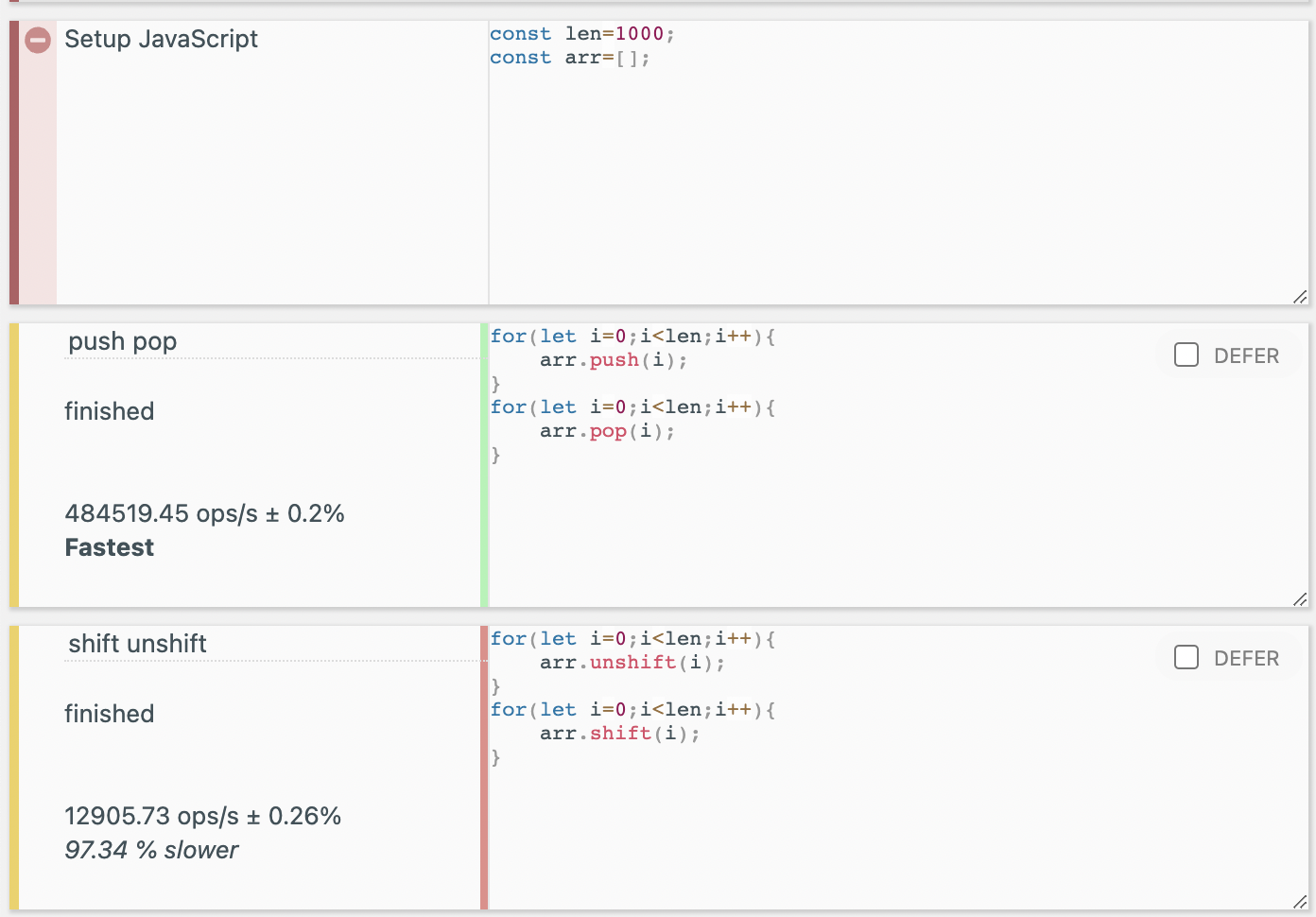
Additionally, benchmarks for 10,000 and 100,000 iterations showed that while the time taken for push and pop increased linearly with the number of repetitions, the time for shift and unshift increased significantly. It appears that shift and unshift actually exhibit a time complexity close to O(n).
10,000 benchmark
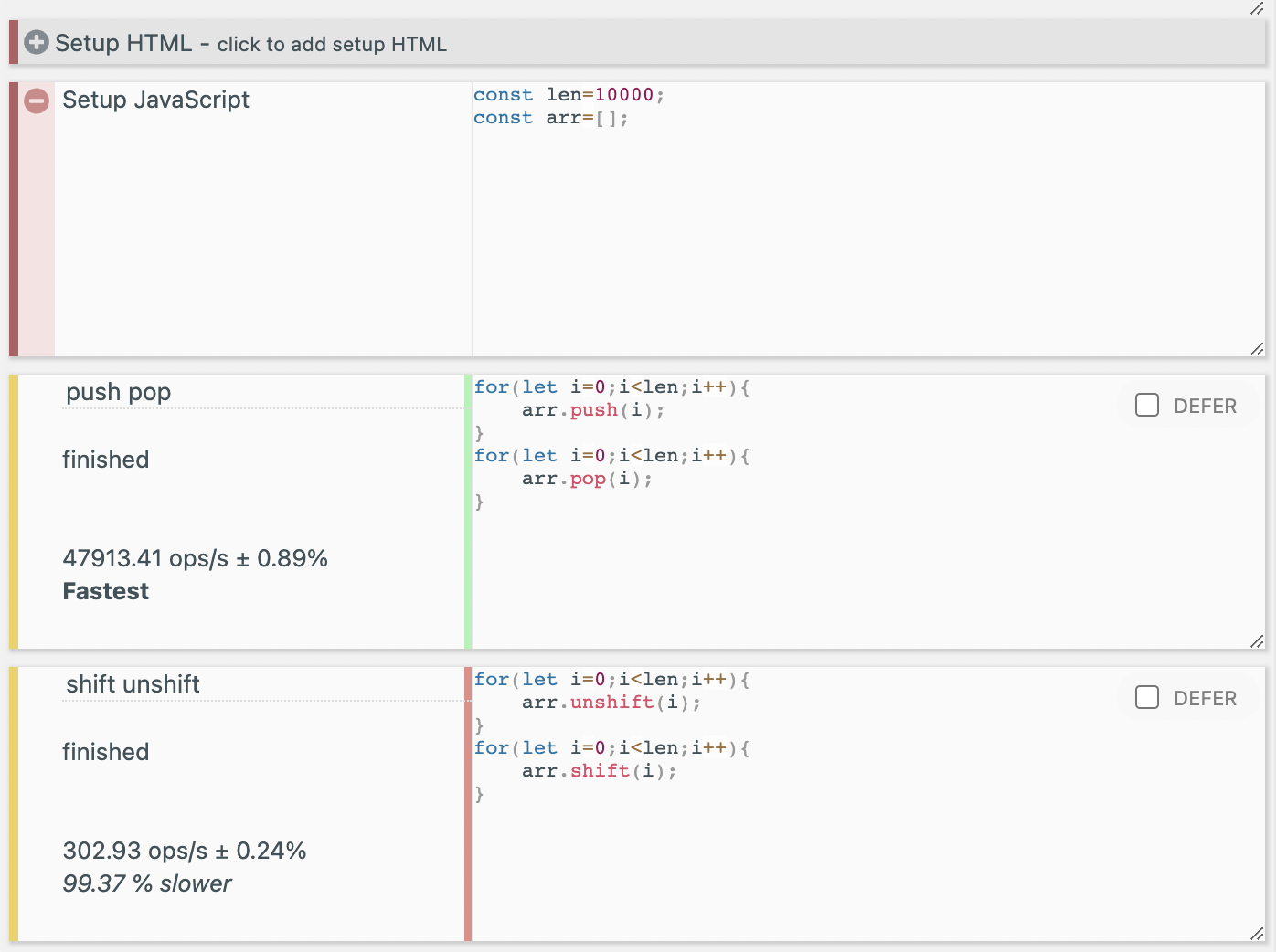
100,000 benchmark