city입니다. 알고리즘을 그럭저럭 오래 해왔는데, 이분 탐색의 원리를 어떻게 이해하는지에 그리고 활용 문제를 접근하는 방식에 대해서 누군가가 물어봐서 써본 글입니다.

기초적인 부분에 대해서는 생략된 부분도 많습니다. 때문에 kks227님의 블로그 글과 같은 좋은 참고자료들이 많으니 같이 보면 좋을 것 같습니다.

글에 사용한 그림들은 excalidraw를 사용하여 직접 그렸습니다.

1. 이분 탐색의 기초

이분 탐색은 기본적으로 정렬된 원소들 사이에서 특정 원소를 찾는 알고리즘입니다.

1.1. 코드

정렬된 arr배열에서 target값을 찾는 코드라면 대략 다음과 같은 코드로 짤 수 있습니다. C++ 기준입니다. 물론 다른 언어라도 논리는 똑같습니다.

while(low<=high) {
  int mid = (low+high)/2;
  if(arr[mid]==target) {
    return mid;
  } else if(arr[mid]>target) {
    high = mid-1;
  } else {
    low = mid+1;
  }
}

1.2. 원리

이것의 핵심 아이디어는 우리가 찾는 값이 존재할 수 있는 탐색 구간을 반씩 줄여 나간다는 것입니다.

처음 탐색을 시작할 때를 생각해 봅시다. arr의 크기가 n이라면 우리가 찾는 값이 있을 수 있는 구간은 arr[0]부터 arr[n-1]까지입니다. 그리고 위의 알고리즘대로라면 arr[(n-1)/2]와 target을 비교하게 될 것입니다.

그런데 배열이 정렬되어 있다는 것을 생각해 볼 때, 배열의 모든 값은 arr[mid]와의 비교를 통해 다음과 같은 두 구간으로 나눌 수 있습니다.

(그럼 mid인덱스는 어느 쪽 구간에 속하는지 의문이 들 수 있습니다. 일단 넘어가도 되는 부분이긴 한데 위와 같은 닫힌 구간 구현에서는 둘 중 어디에도 속하지 않고, 이후에 볼 반열림 구간 [s,e)로 구현할 시에는 오른쪽 부분에 속하게 됩니다.)

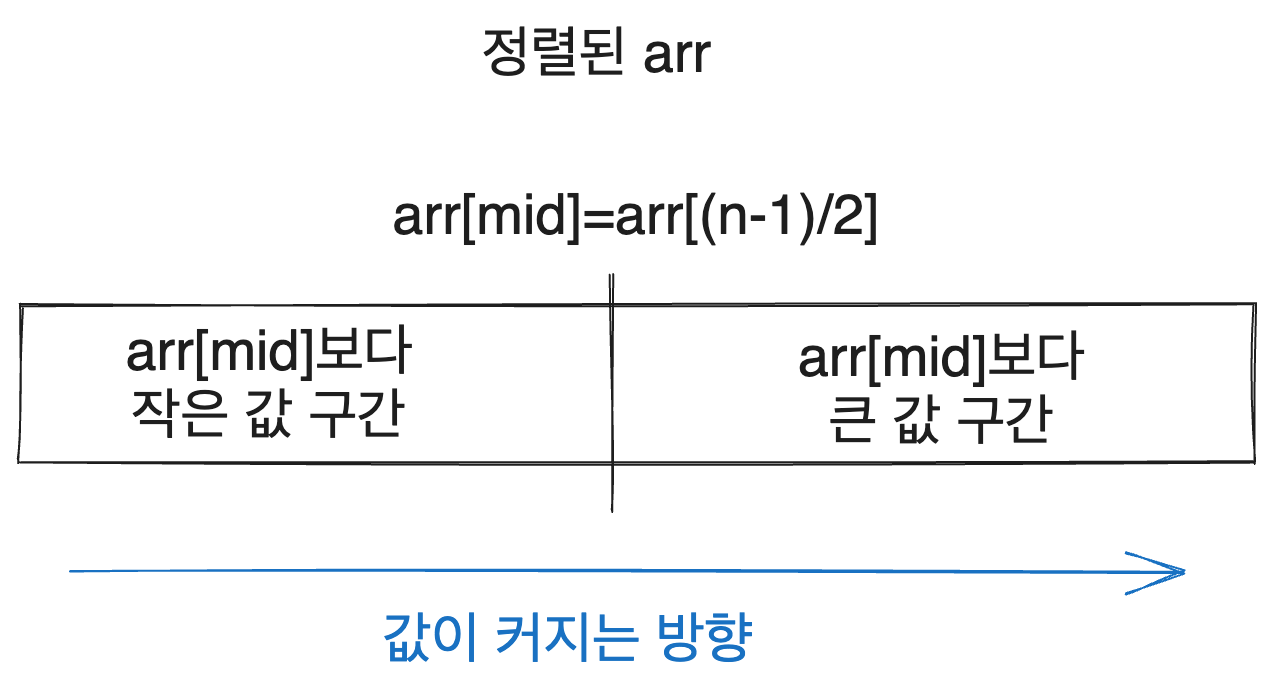
그럼 우리는 찾는 값 target이 arr[mid]보다 작은지 큰지만 비교하면 target이 존재할 수 있는 구간을 반으로 줄일 수 있습니다. target이 arr[mid]보다 작다면 mid인덱스보다 작은 인덱스에 존재할 것이고 크다면 mid인덱스보다 큰 인덱스에 존재할 것이기 때문입니다.

만약 target==arr[mid]라면 우리는 target을 찾은 것이므로 바로 mid를 리턴하면 되고요.

정렬된 배열에서는 이런 식으로 target이 존재할 수 있는 구간을 반씩 줄여 나가면서 탐색할 수 있습니다. 그래서 시간복잡도 O(logN)만에 배열에서 값을 찾을 수 있다는 게 이분 탐색의 핵심 아이디어입니다.

즉 늘 다음과 같은 상황에서 탐색을 진행하게 됩니다.

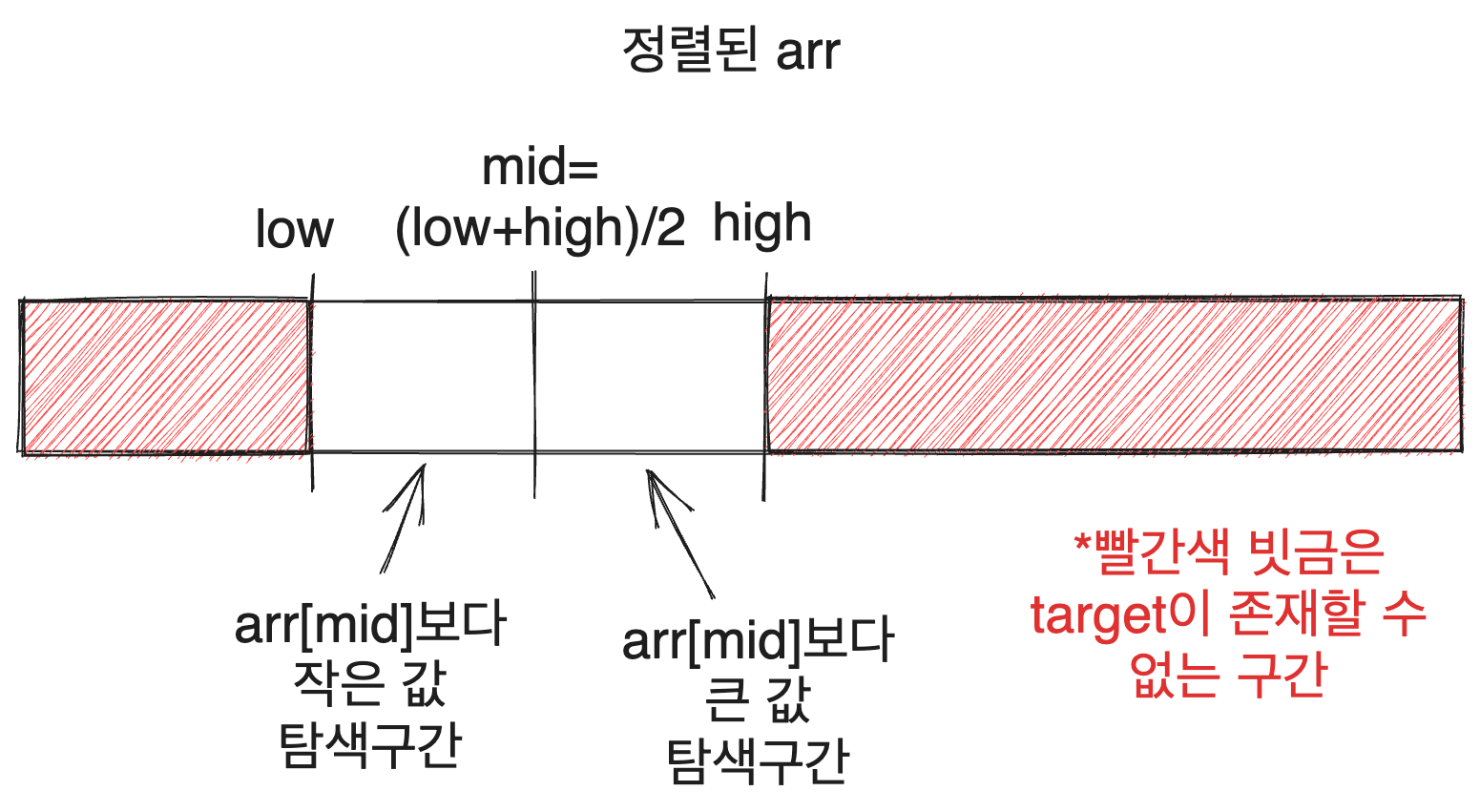
그럼 탐색 구간을 구체적으로 어떻게 좁히느냐? 위의 이분탐색 코드는 설명한 두 가지 경우에 따라 low를 조절하거나 high를 조절해서 탐색 구간을 좁혀 나갑니다.

만약 target이 arr[mid]보다 작다면 target을 찾기 위해 arr[mid]의 왼쪽 구간을 탐색해야 하므로 탐색 구간의 상한인 high를 줄이고, target이 arr[mid]보다 크다면 arr[mid]의 오른쪽 구간을 탐색해야 하므로 탐색 구간의 하한인 low를 늘려줍니다.

이를 반복하다 보면 언젠가는 target을 찾게 되거나 탐색 구간이 더 이상 없어서 target을 찾지 못하게 됩니다.

2. 원리의 확장

2.1. 파라메트릭 서치의 아이디어

하지만 이렇게 배열에서 단순히 하나의 원소를 빠르게 찾아야 하는 경우는 너무 한정적입니다. 실생활이나 문제풀이에서도 이렇게 단순한 경우는 거의 없습니다.

이 아이디어를 좀더 확장해서 활용하기 위해 주목할 것은 우리가 배열이 정렬되어 있다는 것을 활용해서 mid인덱스를 기준으로 한쪽에는 target이 있고, 한쪽에는 target이 없다'라는 것을 알 수 있었고 그로 인해 탐색 공간을 반씩 줄여 나갈 수 있었다는 것입니다.

이 말을 반대로 말하면 탐색 구간을 어떤 기준으로 반씩 줄여 가며 무언가를 찾을 수 있는 작업이라면 이분 탐색을 생각해 볼 수 있다는 이야기입니다. 여기서 파라메트릭 서치의 아이디어가 나옵니다.

가령 arr배열의 0번부터 n-1번 인덱스 중 target을 찾는 것이 아니라 target보다 큰 첫번째 원소의 인덱스를 찾는 문제라고 해봅시다. 이는 원소에 대한 탐색 자체보다 좀 더 넓은 범위를 커버하는 문제입니다.

우리는 그럼 arr이 두 부분으로 나누어져 있다고 생각할 수 있습니다.

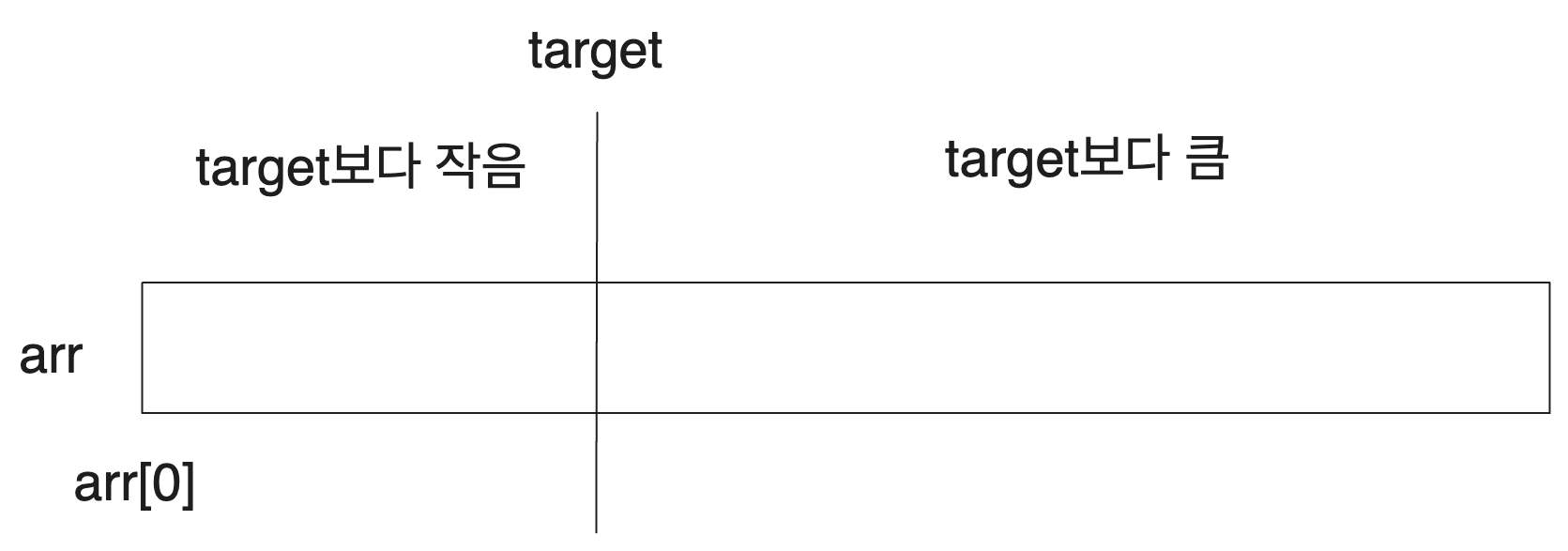
그럼 우리는 arr의 어떤 특정 값이 target보다 작은지 큰지만 판정하면 우린 해당 값이 우리가 찾는 'target보다 큰 첫번째 원소의 인덱스'보다 왼쪽에 있는지 오른쪽에 있는지를 알 수 있습니다.

이를 이용하면 우리는 경계를 찾아야 하는 탐색 구간을 반씩 줄여 나갈 수 있고 따라서 이분탐색의 아이디어로 문제를 풀 수 있습니다.

이렇게 문제를 푸는 방식을 파라메트릭 서치, 즉 매개 변수 탐색이라고도 합니다. 최적화 문제를 결정 문제로 바꿔 푸는 거라고 멋지게 말할 수도 있지만 그 말이 원리만큼 중요하다고 생각하지는 않습니다.

2.2. 파라메트릭 서치

이를 좀더 일반화해 보겠습니다. 우리는 구간 [low, high]에 대해서 생각합니다. 그리고 어떤 결정 문제가 있어서 어떤 특정 자연수 x($low \le x \le high$)에 대해서 x보다 작거나 같은 자연수들에서는 true이고, x보다 큰 자연수들에서는 false라고 해봅시다. 우리는 이 x를 구하고자 합니다.

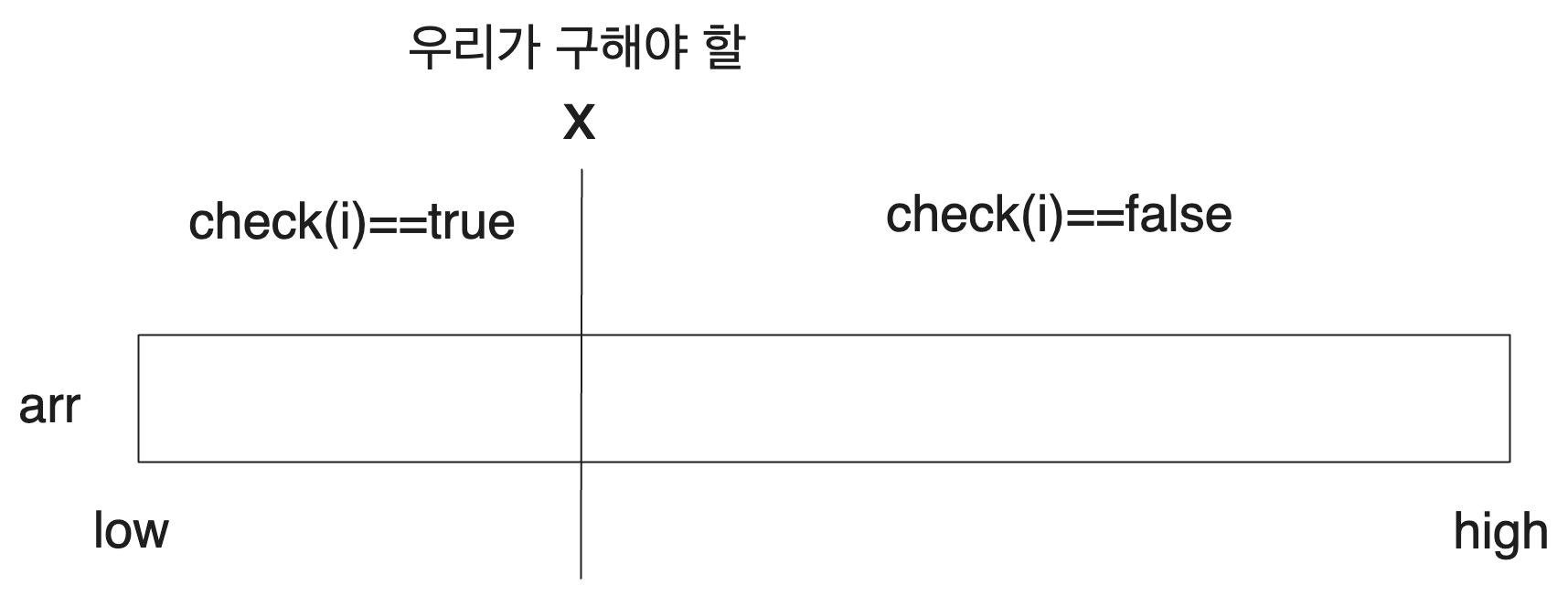
그럼 우리는 우리는 mid=(low+high)/2에 대해 check이 true인지를 기반으로 우리가 구해야 할 값이 mid보다 작은지 큰지를 판단할 수 있습니다.

만약 mid에서 check가 false라고 해봅시다. 그러면 다음과 같은 상황일 것입니다.

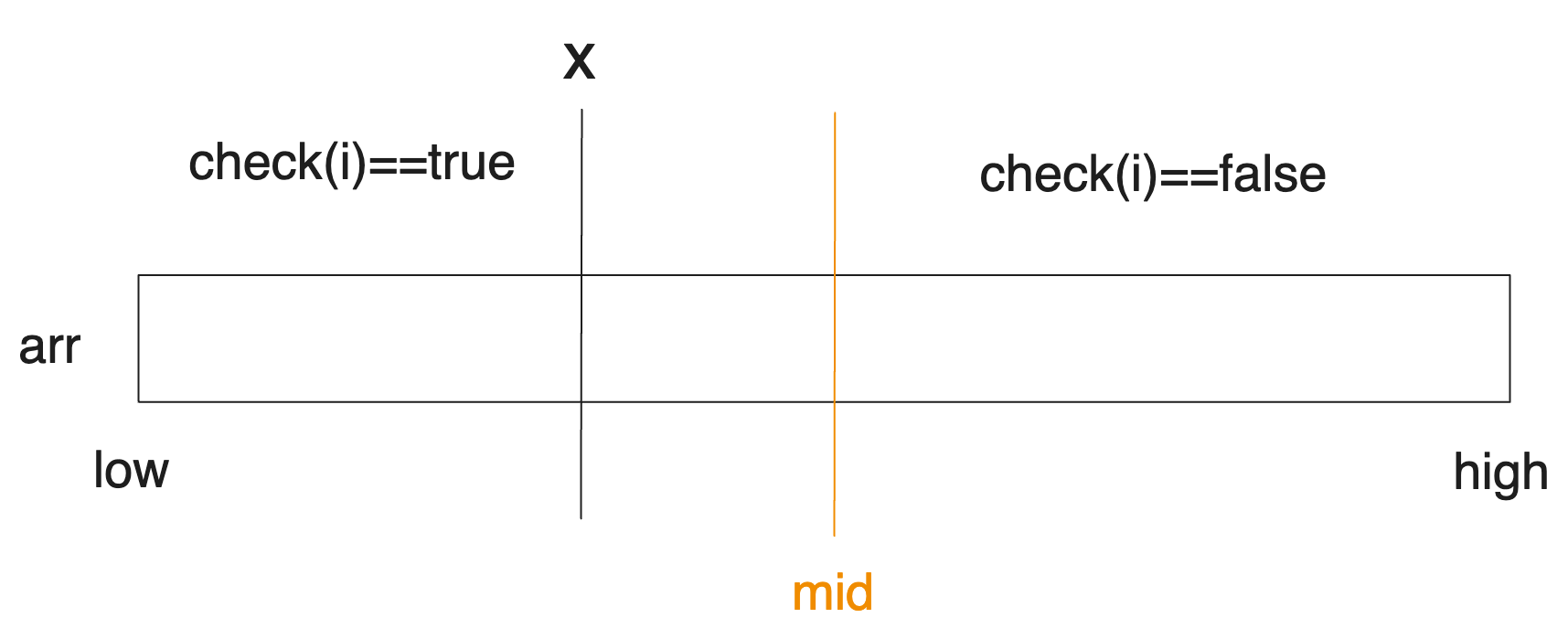
그럼 그림만 보아도, 우리는 x가 mid보다 작은 쪽에 있다는 것을 알 수 있습니다. 만약 반대로 mid에서 check가 true라면 x는 mid보다 큰 쪽에 있을 것입니다. 이를 이용해 탐색 구간을 업데이트해 나갑니다. 다음 섹션에서 더 자세히 보겠습니다.

2.3. 코드와 함께 자세히 보기

코드와 함께 보면 다음과 같습니다. 나올 수 있는 자연수의 하한을 low, 상한을 high라고 하면, 경계선을 찾는 코드는 대강 이럴 것입니다. check(i)==true인 구간의 상한 x를 찾습니다.

while(low<=high){
  int mid = (low+high)/2;
  // A가 mid에서 가능하다
  if(check(mid)){
    low = mid+1;
  }else{
    high = mid-1;
  }
}
return high;

A가 mid에서 가능하다면 즉 check(mid)가 true라면 x는 mid의 오른쪽에 있을 것입니다. 다음과 같은 상황인 거죠.

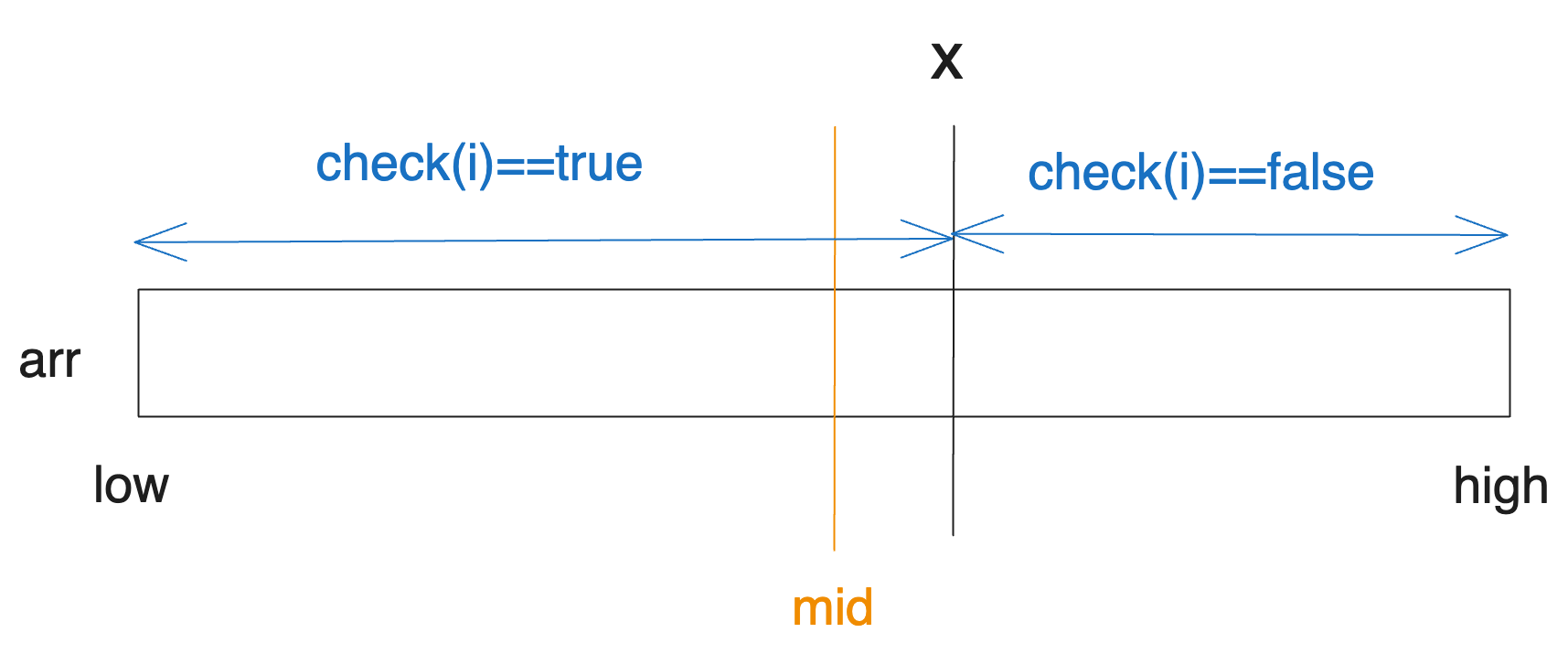
따라서 오른쪽 구간의 탐색을 위해 low를 mid+1로 업데이트해주는 것입니다. 그러고 나면 다음 탐색 구간은 반으로 줄게 됩니다.

반대로 check가 mid에서 false라면 x는 mid의 왼쪽에 있을 수밖에 없습니다. 다음과 같은 상황에서만 mid에서 check가 false일 수 있기 때문입니다.

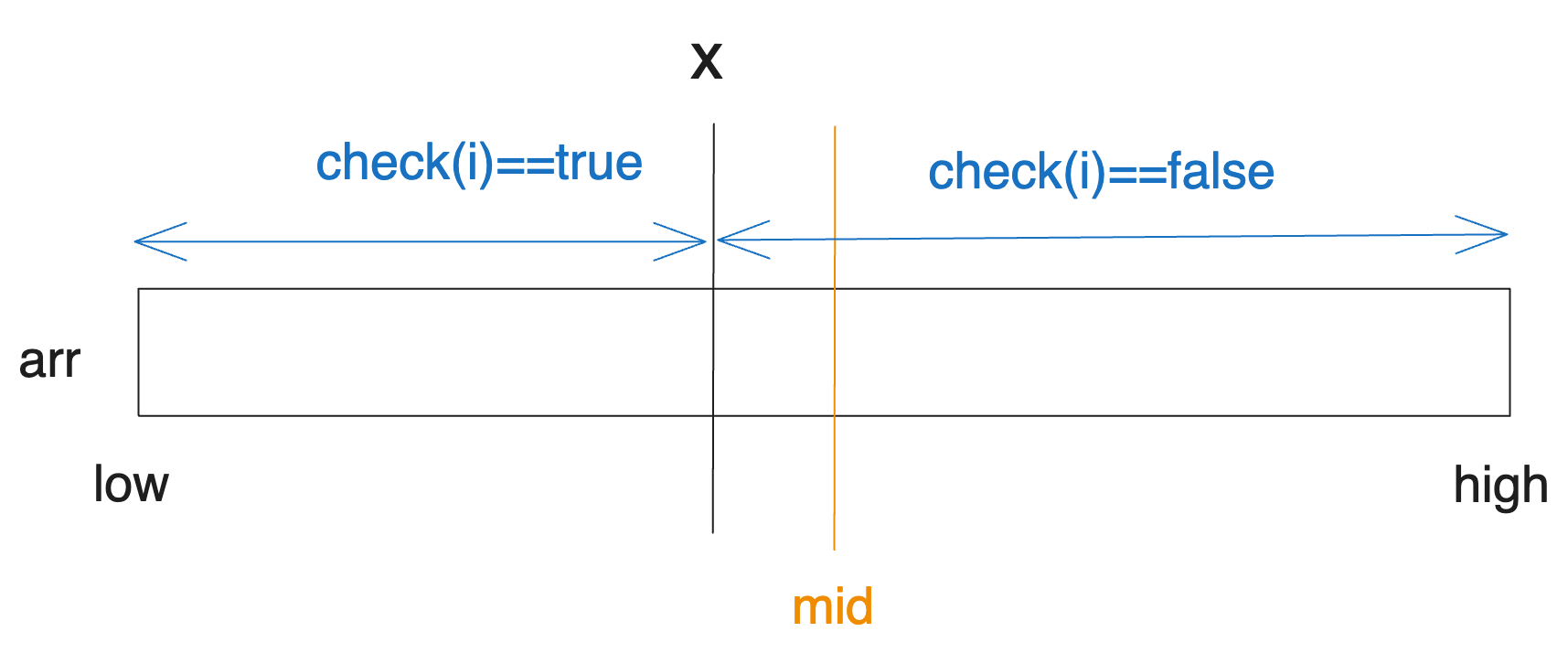
따라서 왼쪽 구간의 탐색을 위해 high를 mid-1로 업데이트해주는 것입니다.

이를 반복하다 보면 x를 찾을 수 있습니다!

3. 더 깊이 이해하기

이분탐색에 대한 자료는 워낙 많기 때문에 이 정도 이해는 사실 꽤 많은 분들이 하고 계십니다. 하지만 가장 헷갈리는 부분은 이런 거라고 생각합니다. 이로 인해 답에 1차이가 나는 등의 문제를 off by one이라고도 하는 것 같습니다.

while(low<=high) vs while(low<high)
low 출력 vs high 출력
(lower와 upper, l과 r, s와 e등의 다른 변수명을 쓰는 분들도 있지만 가리키는 건 어차피 똑같으니 low, high로 하겠습니다)

많은 분들이 그렇듯이 저도 알고리즘을 처음 시작한 지 몇 달 안 되어 이분 탐색을 배웠지만 이런 것들을 잘 이해하기까지는 1년도 넘게 걸린 것 같습니다.

따라서 먼저 제가 사용하는 방식에서 저런 부분들을 어떻게 다루는지 설명하도록 하겠습니다. 그리고 다음 글에서는 다른 방식도 소개해 보도록 하겠습니다.

3.1. 구현 이해하기

문제 조건에 따라 조금씩 달라지지만 어떤 문제 check가 true인 구간의 최댓값 혹은 최솟값을 찾는 파라메트릭 서치에 제가 흔히 쓰는 코드는 다음과 같습니다. 위에 쓴 것과 같습니다.

while(low<=high){
  int mid=(low+high)/2;
  if(check(mid)){
    low=mid+1;
  }
  else{
    high=mid-1;
  }
}

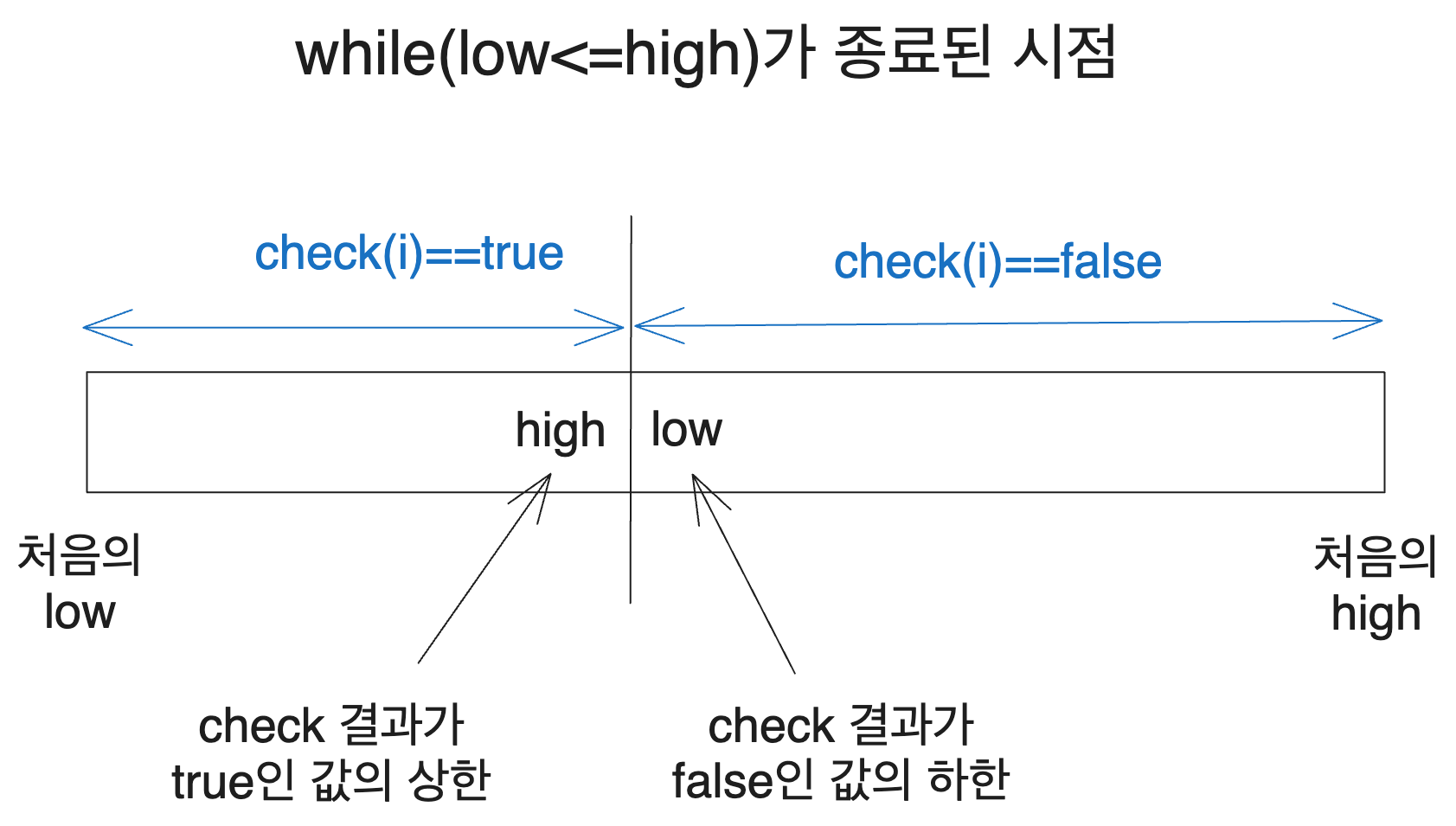
그럼 이 while문은 어느 시점에 종료될까요? while은 low <= high일 때 body를 실행하니까 while이 종료되었다는 것은 low > high가 되었다는 뜻일 겁니다.

그리고 탐색 구간의 길이는 계속 작아져서 결국 1이 되었을 테니 low > high일 때 둘의 차이는 1이 될 것입니다.

다음 그림의 상황은 low == high+1이 되어 while이 종료된 상황입니다.

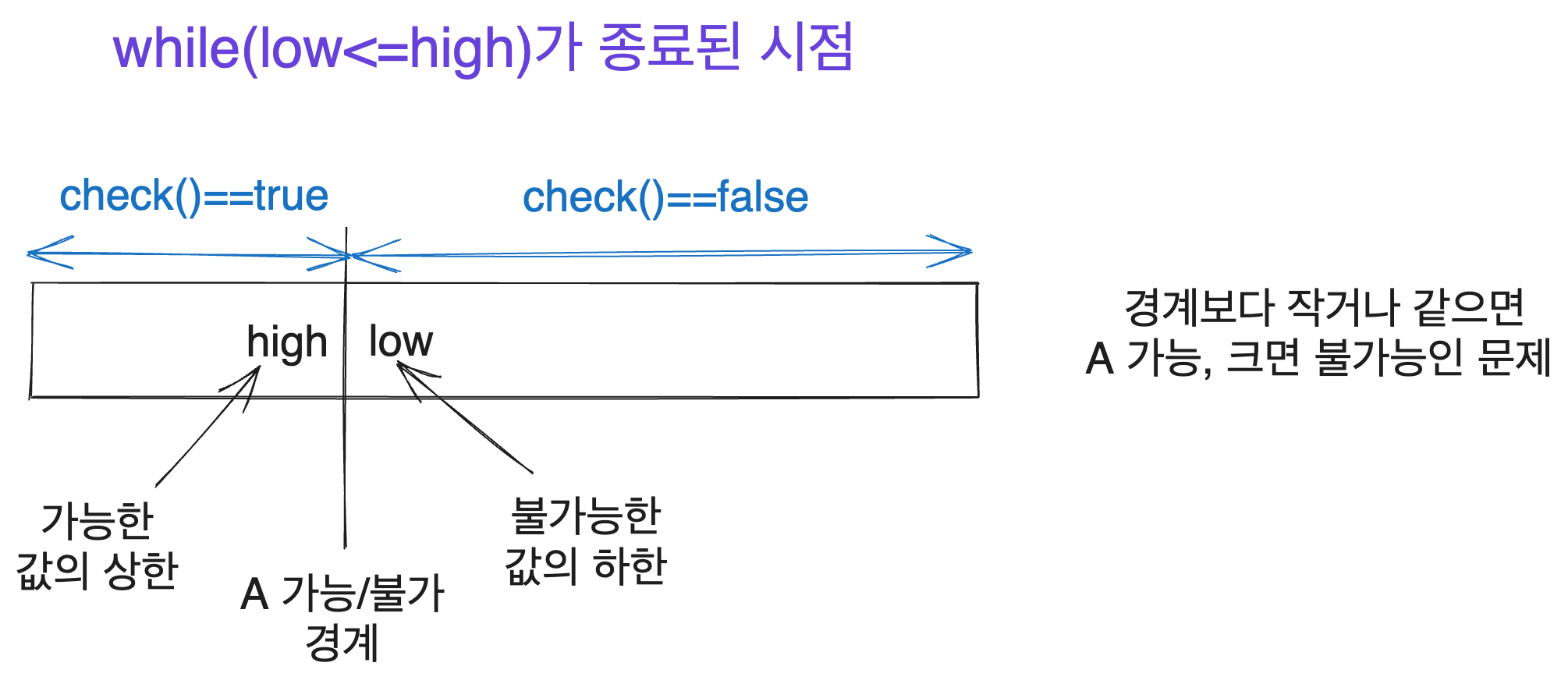
즉 탐색이 종료된 시점에서 high는 check(i)==true인 구간의 상한을, low는 check(i)==true인 구간의 하한을 나타내게 됩니다.

3.2. 문제로 생각해보기

유명한 파라메트릭 서치 문제인 1654번 랜선 자르기를 봅시다.

특정 경계 수보다 작거나 같으면 문제의 조건을 만족시킬 수 있고 크면 문제 조건을 만족시킬 수 없습니다. K개의 랜선들을 같은 길이로 잘라서 N개의 랜선을 만들어야 하고 그럴 수 있는 최대 랜선 길이를 구해야 한다는 문제 조건을 생각해 보면 당연합니다.

만약 K개의 랜선을 각각 X 길이로 잘라서 N개의 랜선을 만드는 것이 가능하다면 X보다 작은 길이로도 그것이 가능하고, K개의 랜선을 Y 길이로 잘라서 N개의 랜선을 만드는 것이 불가능하다면 Y보다 큰 길이로도 그것이 불가능하기 때문입니다.

만약 어떤 길이 L이 있어서 우리가 길이 L의 랜선을 N개 만들어서 문제 조건을 만족시킬 수 있다고 합시다. 그러면 L보다 작은 길이의 랜선을 N개 만드는 건 굳이 수학적 증명이 없이도 가능하다는 걸 쉽게 깨달을 수 있습니다. N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다는 문제 조건이 있기 때문에~

그러므로 이 문제는 경계선을 나타내는 자연수보다 작거나 같으면 가능, 크면 불가능인 상황이고 그 '가능한 구간'의 최댓값을 찾는 문제입니다.

즉 이 문제와 같은 경우 가능한 구간의 상한인 high를 출력하면 되는 문제입니다(심지어 문제 설명에도 '최댓값을 구하라'고 친절하게 말해 줍니다).

즉 입력을 제외한 랜선 자르기 문제에서 이분 탐색 부분만 따로 떼어서 적어보면 다음과 같습니다. high를 출력하면 됩니다.

while(low<=high){
    ll mid=(low+high)/2;
    if(check(mid)){
        low=mid+1;
    }
    else{
        high=mid-1;
    }
}
cout<<high<<"\n";

반면 1072번 게임과 같은 문제에서는 게임을 최소 몇 번 더 해야 Z가 변하는지 즉 가능한 구간의 최솟값을 찾는 문제이므로 low를 출력해야 합니다.

3.3. 여담

이렇게 구간을 줄여나가는 아이디어를 통해서 할 수 있는 게 정말 많습니다. 구간합의 홀짝성이 달라지는 것을 이용해서 이분탐색을 한다든지, 아예 구간을 3개로 나눠서 극점을 찾는 삼분 탐색을 한다든지 아니면 자연수 대신 실수도 어쨌든 정렬되어 있다고 생각할 수 있으므로 이를 이분탐색한다든지 등등...

또한 가능 여부를 따지는 부분도 중요하지만 위에서는 그냥 check함수로 퉁쳤습니다. 이것도 사실 문제를 풀 때 엄청 어려운 포인트가 될 수도 있습니다. 1637번 날카로운 눈같은 문제를 보면서 이분탐색을 바로 떠올리기는 쉽지 않고 판정 방식을 떠올리기도 쉽지 않습니다. 이런 부분들도 나중에 기회가 되면 쓰도록 하겠습니다.

3.4. 다른 구현 한 가지

다른 구현들에 대해서는 본격적으로 다음 글에서 다룰 것입니다. 하지만 간단한 바리에이션 하나를 여기서 소개합니다.

구간을 따지는 방식을 바꾸는 것은 아니고, 정답이 될 수 있는 값을 계속 업데이트하는 것입니다. 다음과 같이 말입니다.

ll ans=min_value;
while(low<=high){
    ll mid=(low+high)/2;
    if(check(mid)){
        low=mid+1;
        ans=max(ans, mid);
    }
    else{
        high=mid-1;
    }
}
cout<<ans<<"\n";

이렇게 하면 무조건 가능 구간의 상한이 ans에 들어갑니다. 이분탐색 하는 동안 가능 구간의 상한 값이 ans에 한 번은 들어갈 수밖에 없고 이는 들어가는 값 중 최댓값이기 때문입니다.

구간의 가능성이 반대라면 적당히 ans=min(ans, mid)으로 바꾸고 위치도 변경하면 됩니다. 원리를 생각하면 쉽게 할 수 있습니다. 이렇게 이분탐색을 다루는 분들도 몇 분 보았고 구간이 줄어드는 원리 이해에 도움이 된다고 생각해서 이 글에 소개합니다.

4. 정리

이분 탐색을 활용해서 문제를 풀 때의 핵심은 '한쪽 구간은 뭔가가 되고, 한쪽 구간은 안 된다. 따라서 어떤 한 값의 가능 여부를 알면 그 값을 기준으로 어떤 구간을 탐색할지 결정할 수 있다.'라는 것입니다.

그렇게 탐색 구간을 줄여가다 보면 결국 경계선을 찾을 수 있는데요. 이때 경계선을 찾는 while문이 언제 종료되는지를 따져 보면 우리는 high와 low중 어떤 값이 필요한지를 알 수 있습니다. 닫힌 구간으로 구현하건 반열린 구간으로 구현하건 마찬가지입니다.

우리가 어떤 가능성을 따지고 있는지, 그리고 while문이 어떤 조건일 때 종료될지를 생각하며 이분 탐색에 접근합시다.

그리고 반대로, 어떤 값을 경계로 어떤 기준의 가능/불가능 여부가 바뀐다면(x보다 작거나 같은 값에 대해서는 문제 조건이 가능한데, x보다 크면 안 되고 이때의 x값을 찾아라~하는 식, 혹은 문제를 잘 생각해 보면 그런 문제로 환원시킬 수 있는 문제)이분 탐색을 한번 생각해 봅시다.

참고

https://codeforces.com/blog/entry/96699