JS 탐구생활 - 배열 삽입 메서드의 시간복잡도
1. 들어가며
Javascript의 배열은 실제 배열이 아니다. 그럼 배열의 삽입 메서드들의 시간복잡도는 어떻게 될까?
1.1. 의문
일반적인 언어에서 배열은 연속된 메모리 공간에 원소들을 저장하는 자료구조이다. 따라서 C 등의 언어에서 배열은 얼만큼의 연속된 메모리 공간을 사용할 것인지 고정된 크기로 선언하며 일반적으로 배열의 크기를 변경하는 것은 불가능하다.
예를 들어 C언어에서 크기 10의 배열을 선언하면 이제 배열 크기를 11 혹은 다른 크기로 변경할 수는 없다. 동적 배열이라고 해도 새로운 배열을 할당 후 기존 배열을 복사해야 한다.
하지만 Javascript의 배열은 실제 배열이 아니다. Javascript의 배열은 객체이며, 배열의 인덱스는 객체의 속성이다. 인덱스가 아니라 다른 속성을 추가하는 것도 가능하며 배열의 크기를 늘리거나 줄이는 것도 가능하다. push, pop, shift, unshift같은 메서드들도 있다.
물론 다른 언어들에서도 비슷한 자료구조들이 있다. Python의 리스트나 C++의 Vector등이 동적 배열로 구현되어 있다. 하지만 key-value쌍을 갖는 Javascript의 배열과는 묘하게 다르다.
그럼 Javascript의 배열의 삽입 메서드들의 시간복잡도는 어떻게 될까? C++의 Vector와 같은 동적 배열과 비슷한 시간복잡도를 가질까? 아니면 다른 자료구조를 사용해서 O(1)에 양쪽 삽입이 가능할까?
따라서 이 글에서는 모든 Javascript 엔진이 따라야 하는 명세와 벤치마크를 기반으로 Javascript 배열의 삽입 메서드들의 시간복잡도를 분석해 보았다.
이후 Javascript에서 배열의 구현을 구체적으로 다루는 글에서 보겠지만 Javascript의 배열은 대부분의 엔진에서 우리가 아는, 연속된 메모리 공간을 차지하는 그런 배열로 구현되어 있다. 하지만 다른 구현체도 있고 특정 경우에 내부적으로 다른 자료구조로 변환되기도 하므로 이 글에서는 명세를 기반으로 분석해 보았다.
2. 명세 탐구
2.1. push
배열의 push메서드는 배열의 맨 뒤에 원소를 추가한다. Array.prototype.push(element1, element2, ...)와 같은 형태로 나타나서 인수로 받은 것들을 모두 배열 끝에 추가한다. 그리고 배열의 새 길이를 반환한다.
ECMA-262의 Array.prototype.push 명세는 다음과 같다.

에러 체킹 등을 걷어내고 로직만 보면, 모든 인수에 대해서 배열의 끝에 해당 인수를 추가하고 배열 길이를 1 늘리는 동작을 반복하는 것이다. 따라서 시간복잡도는 O(인자 개수)라고 할 수 있고 인자가 상수 개수라면 O(1)이다.
2.2. pop
Array.prototype.pop은 배열의 맨 끝, 그러니까 array.length - 1 인덱스의 원소를 제거하고 제거한 그 원소를 반환한다. ECMA-262에서의 명세는 다음과 같다.

배열이 비어 있을 때 undefined를 반환하는 처리가 있긴 하다. 그래도 기본 로직은 배열의 끝 원소를 제거하고 반환하는 것이다. 배열의 다른 원소들에 대해서 어떤 동작을 반복한다든지 하는 건 없다. 따라서 시간복잡도는 O(1)이다.
2.3. unshift
Array.prototype.unshift는 인자로 받은 원소들을 배열의 맨 앞에 추가한다. 그리고 배열의 새 길이를 반환한다. 명세는 다음과 같다.
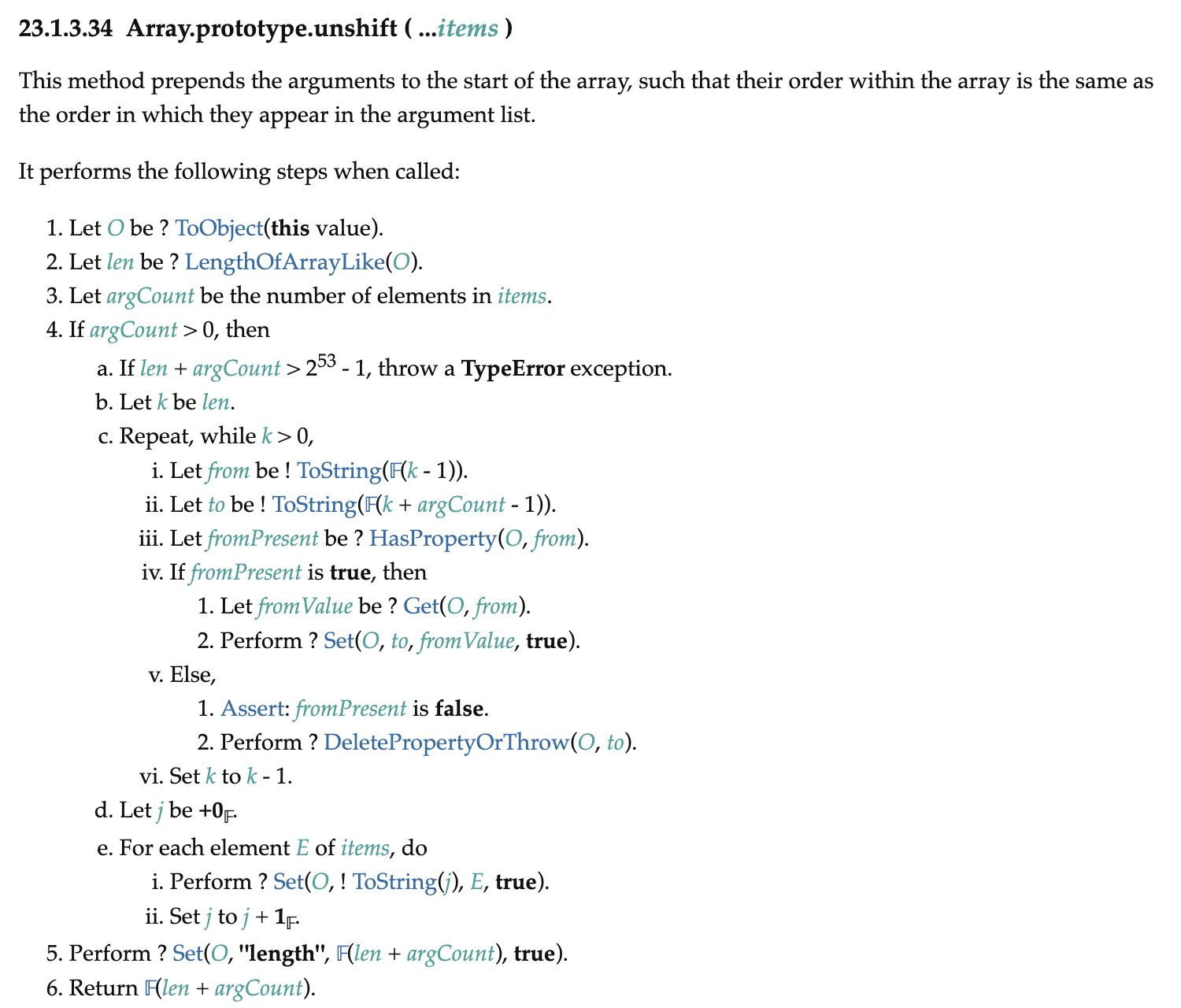
여기서 4.c를 보면 배열에 있던 기존 원소들을 인자 개수인 argCount만큼 뒤로 이동시키는 것을 볼 수 있다. 그리고 인자로 받은 원소들을 배열의 앞(기존 원소들이 이동했으니 이제 비어 있다)에 추가한다.
이 함수의 시간복잡도는 O(기존의 배열 길이 + unshift 인자 개수)이고, 일반적으로 unshift의 인자 갯수가 기존 배열 길이보다 적으므로 시간복잡도는 O(n)이라고 할 수 있다.
2.4. shift
Array.prototype.shift는 배열의 맨 앞에 있는 원소를 제거한다. 그리고 제거한 원소를 반환한다. 명세는 다음과 같다.

여기서는 6.을 보면 기존 원소들을 한 칸씩 앞으로 당겨주고 있다. [1, len-1]범위 인덱스의 원소들을 [0, len-2] 인덱스로 한 칸씩 옮겨주는 것이다. 이외에 반복이 적용되는 부분은 없다.
이를 보면 이 함수의 시간복잡도는 O(기존의 배열 길이)이므로 O(n)이라고 할 수 있을 것이다. 기존 배열의 첫 원소는 이후에 반환해야 하기 때문에 4. 에서 보관해 놓고 9. 에서 반환한다.
3. 벤치마크
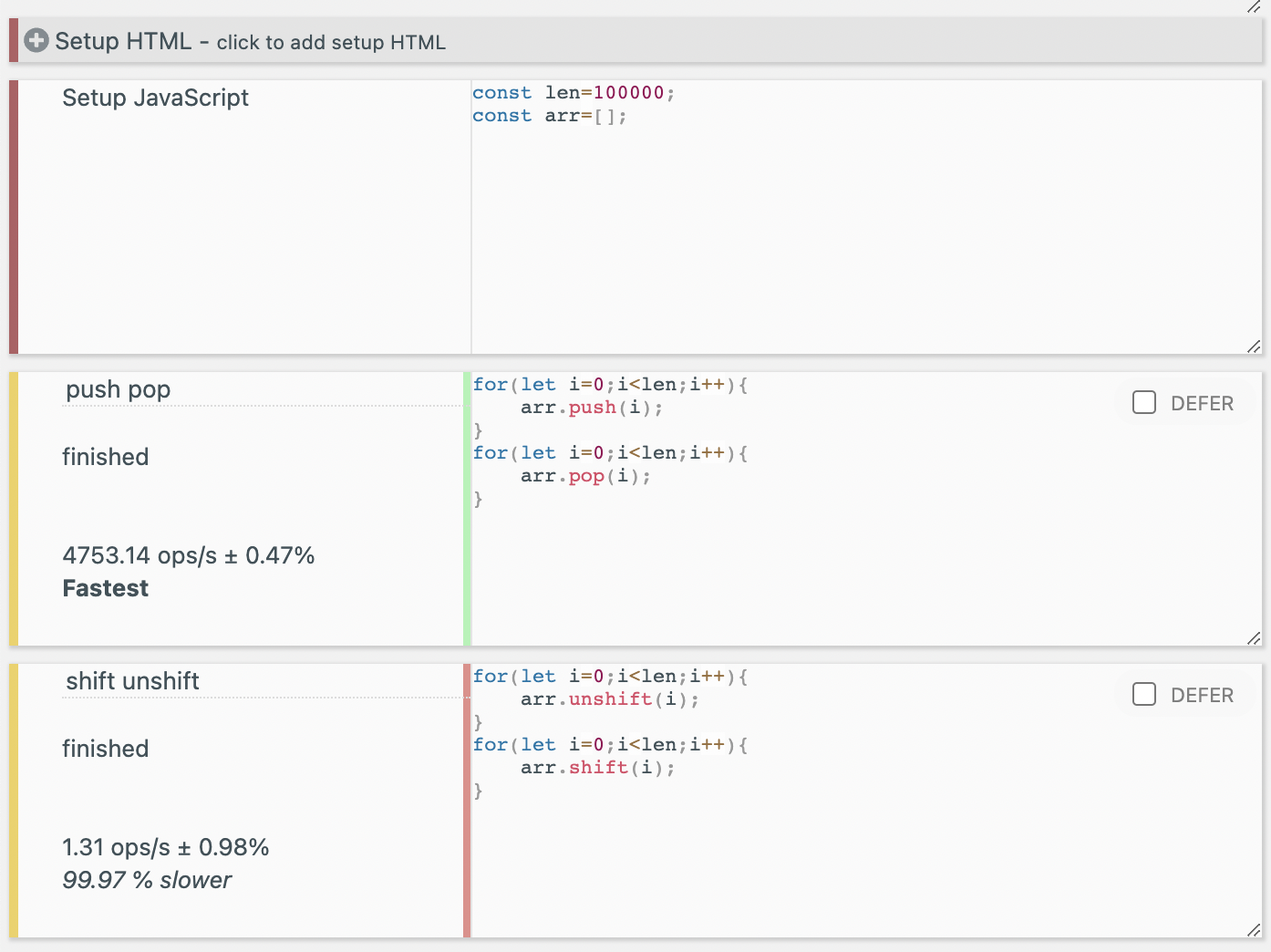
JS 벤치마크 사이트에서 간단히 벤치마크도 해보았다. 일단 가볍게 1000번 정도씩 돌려 보았다. push/pop이 훨씬 빠르다는 것을 알 수 있었다.
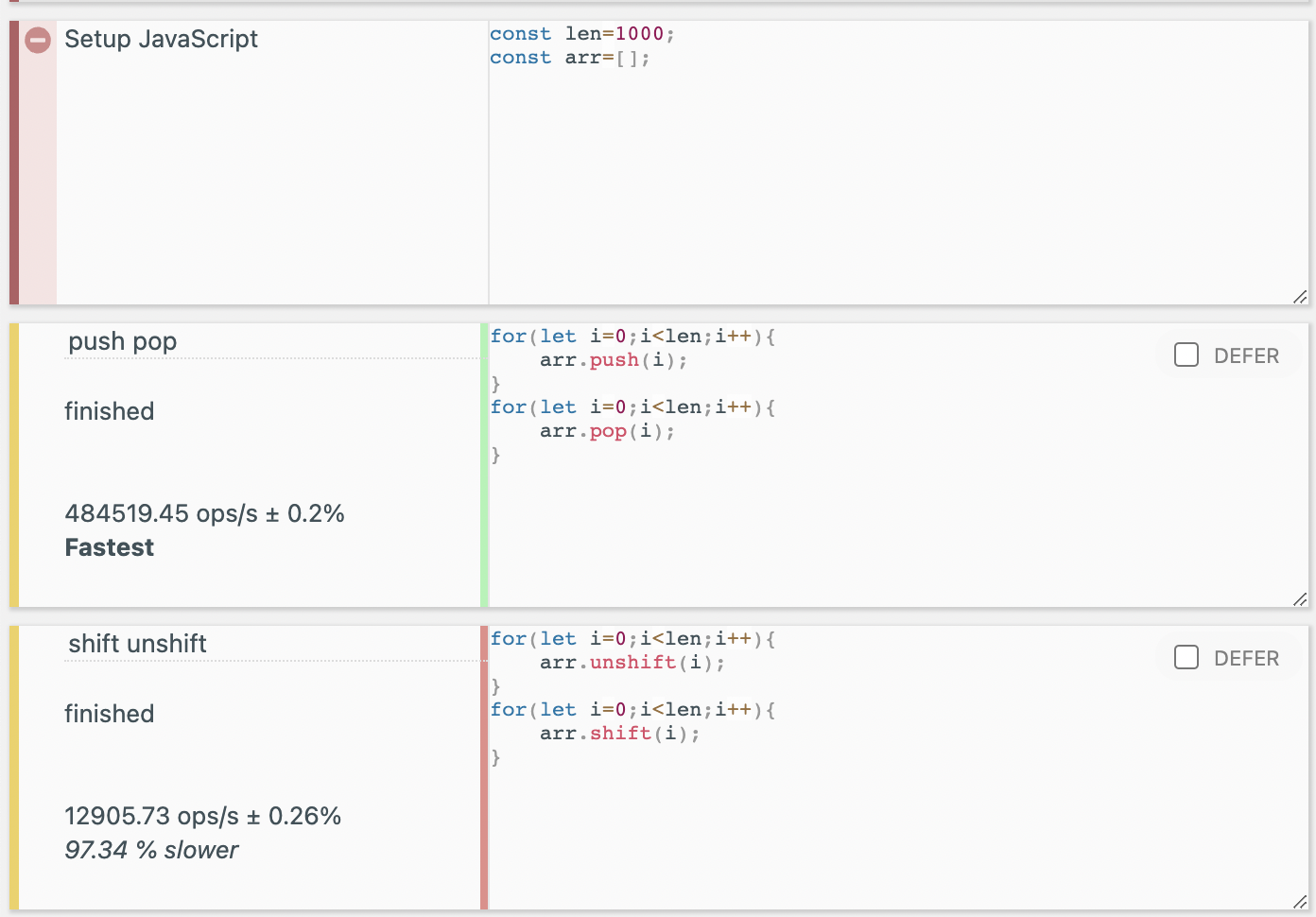
그리고 1만번, 10만번의 벤치마크도 돌려 보았는데 push, pop은 반복 횟수에 따라 걸리는 시간이 선형적으로 증가하는 반면 shift, unshift는 반복 횟수 증가에 따른 경과 시간이 훨씬 더 크게 증가하는 것을 볼 수 있었다. shift, unshift는 실제로도 O(n)에 가까운 시간복잡도를 가지는 것으로 보인다.
1만번 벤치마크
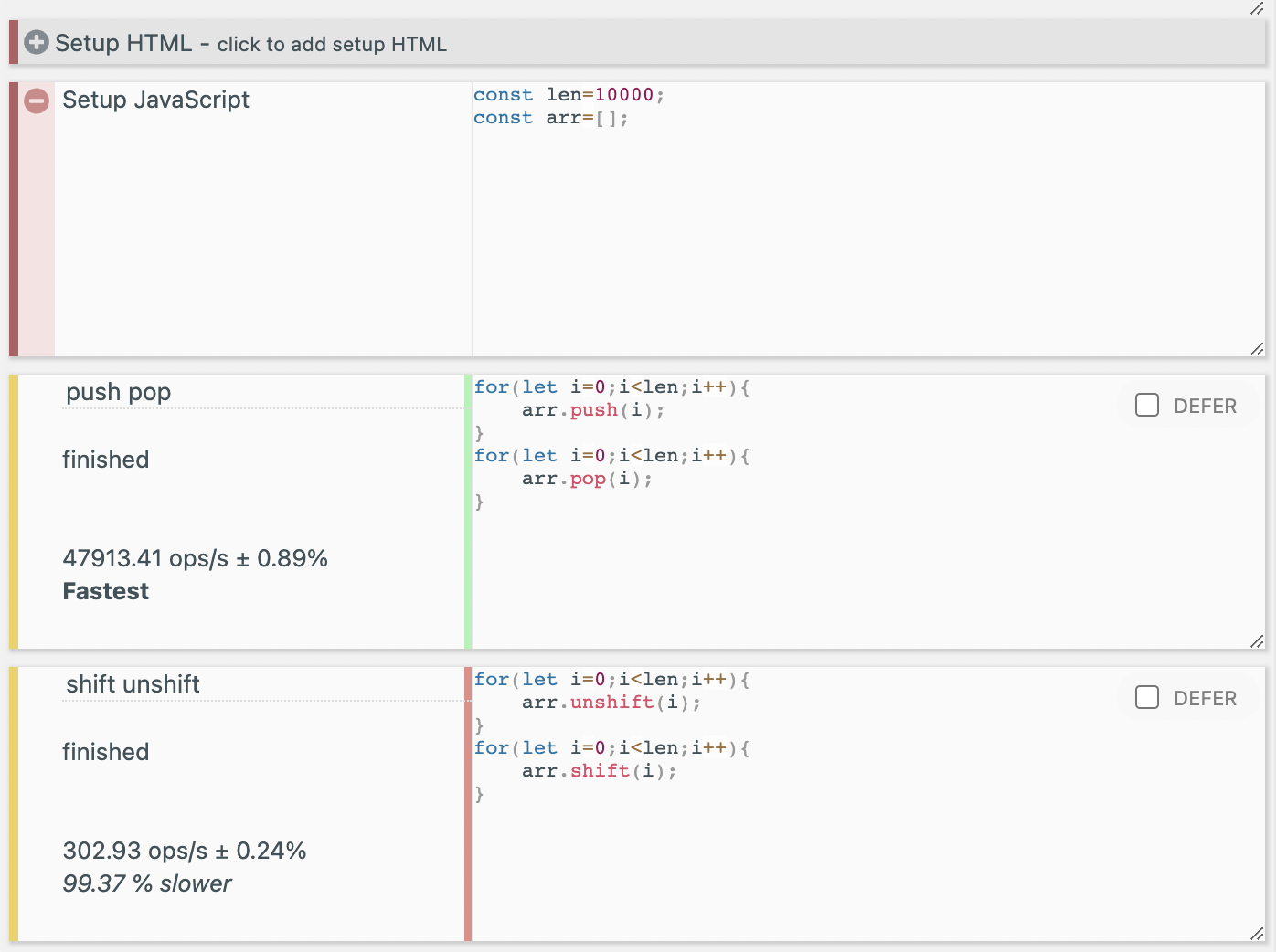
10만번 벤치마크